Intro:
This research project aims to explore a potential new method of encryption utilizing a pair of neural networks. Unlike static key encryption, such as AES-256, this method employs a separate but synchronized pair of neural networks that adapt over time, potentially making decryption significantly more difficult for unintended parties.
Background:
Encryption has been around since the dawn of mankind in various forms. While much less sophisticated and secure, even our Founding Fathers used encryption to protect their messages. Today, encryption is a part of everyday life, as almost everything you do on electronic devices is encrypted. Messages, server requests, and calls are all secured in some way to ensure privacy from criminals and foreign entities. The current industry standard is AES, which stands for Advanced Encryption Standard. On the other hand, neural networks are a relatively new technology that is still being researched and improved to build more effective AI models across various fields, such as computer vision and classification.
Technical Overview:
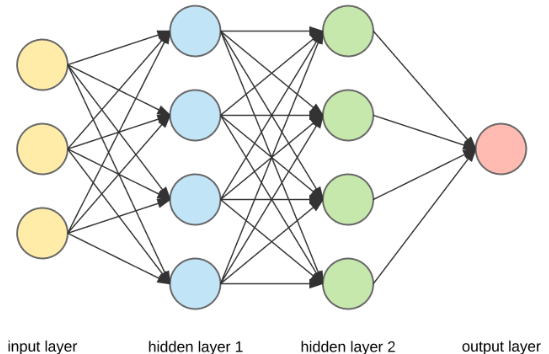
To begin, my project proposes the concept of twin neural networks between communicating computers, where the forward pass propagates the ciphertext. These two networks will establish a connection by exchanging a random seed, which will set the weights to a random value. Then we run the forward pass, which comprises 16 input nodes, 16 hidden nodes, and 16 output nodes, with a total of 512 weights. Furthermore, to prevent simple decryption, I am using a non-linear activation function that computes the inverse tangent of the given number (range ± π/2). From there, we send the ciphertext over the web to the other computer. Since the other computer has an identical neural network, you can calculate the inverse of the weight matrices, apply the inverse of the activation function, and recover the plaintext from the ciphertext. The final step of the process involves adjusting the weights of the twin neural networks in the same random direction. To achieve this, I utilize backpropagation, which employs an error value to change the weights based on the activation, weights, and node values. A random error code will be shared through a key exchange, such as Kyber (not implemented yet); thus, the same plaintext will have a different ciphertext each time.
Comparison: AES-256 vs. Neural Network Encryption
| Feature | AES-256 | Neural Network Encryption |
|---|---|---|
| Brute Force Possibilities | ~1077 (2256) | ~101844 (based on 64-bit double weights × 512 parameters) |
| Speed (Encrypting 16 Characters) | ~0.0001 ms (highly optimized in hardware) |
~0.017 ms (C prototype on CPU) |
| Computational Complexity | 10–14 rounds of bitwise operations | 512-weight forward pass + inverse operations |
| Key Size | 256 bits (32 bytes) | 64 bits (1 double) |
| Key Evolution | Static key per session | Weights evolve per message (via backpropagation) |
| Post-Quantum Resistance | Possibly vulnerable | Planned via Kyber-based key exchange |
| Theoretical Security | Mathematically proven | Experimental Concept |
| Testing & Validation | Extensive proofs and decades of use without fail | Prototype |
| Reliability | Industry-grade | Possible floating point drift |
| Use Case Maturity | Used in the highest security places | Experimental research only |

Outcome:
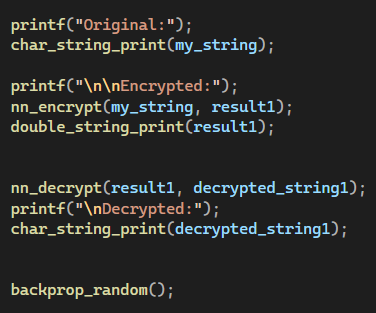
I have successfully developed a working prototype of the twin neural network encryption system. This prototype demonstrates the feasibility of encrypting and decrypting messages using this approach.
Future Work:
Since this project is currently a prototype, I plan to implement and test several new features. For example, I intend to conduct long-term stress tests to evaluate whether floating-point imprecision could cause divergence between the two neural networks, as I have only tested up to approximately 100,000 attempts so far. Additionally, I plan to consult with experts in encryption and cybersecurity to gain valuable insights and identify any potential vulnerabilities. Lastly, I plan to conduct more comprehensive brute force attacks further to assess the security and robustness of this approach.
